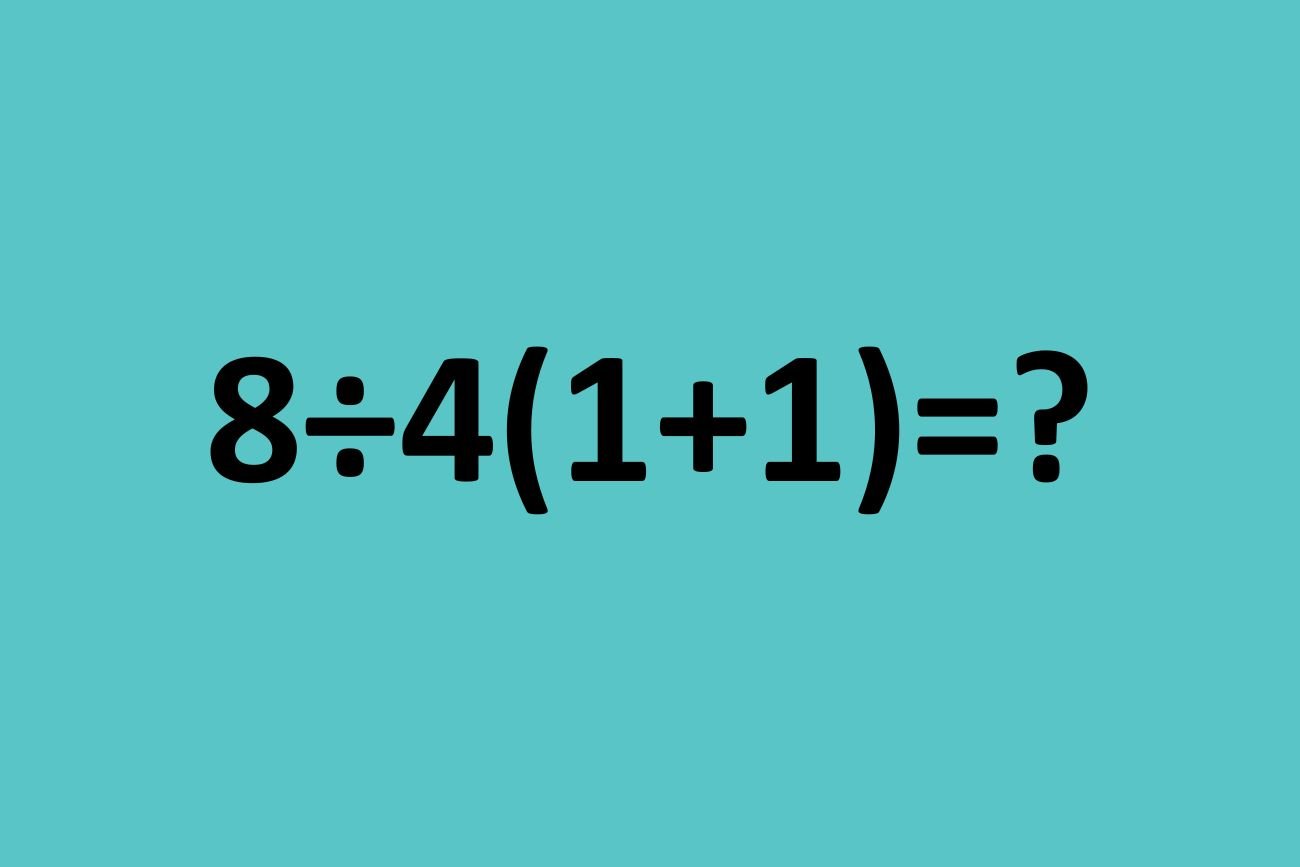
Jaki jest prawidłowy wynik: 1 czy 4? Jeśli poprosicie o rozwiązanie tego równania 4-klasistę, prawdopodobnie udzieli poprawnej odpowiedzi w mniej niż minutę. Dla dorosłych ta zagadka może stanowić jednak wyzwanie – wielu z nas już nie pamięta o prawidłowej kolejności wykonywania działań.
Najbardziej znanym równaniem opartym na podobnym schemacie jest to, o którym pisałyśmy już jakiś czas temu: ile to jest 6÷2(1+2)? Dorośli głowili się, a niektórzy nawet wykłócali z matematykami tłumaczącymi, że jest tylko jedna poprawna odpowiedź. Równanie 8÷4(1+1) nie jest tak popularne, jednak wymaga tej samej wiedzy: znajomości kolejności wykonywania działań, którą poznaje się w 4 klasie szkoły podstawowej.
Jeśli od zakończenia naszej edukacji minęło już kilka ładnych lat, a w dodatku nigdy nie byliśmy orłami z matematyki (gdybym miała wybrać, jaki ptak reprezentuje moje matematyczne umiejętności, prawdopodobnie byłby to pingwin), możemy nie być pewni rozwiązania. Zatem po kolei.
Prawidłowa kolejność wykonywania działań to:
Rozwiązywanie tego zadania należy więc zacząć od wykonania działania w nawiasie. Następnie zostają nam dwa działania: dzielenie i mnożenie. Zgodnie z zasadą, że mają one taki sam priorytet, równanie rozwiązuje się od lewej do prawej strony, zatem najpierw dzielimy, a następnie mnożymy. W tym przykładzie pominięto znak mnożenia, a zamiast niego znajduje się nawias.
8÷4(1+1)=? 8÷4(2)=? 2(2)=4
Prawidłowa odpowiedź to 4.
Choć po wpisaniu równania do wyszukiwarki lub obliczeniu na kalkulatorze uzyskujemy wynik 4, niektórzy są przekonani, że to błąd, a prawidłowa odpowiedź to 1. Taki wynik uzyskamy, jeśli potraktujemy mnożenie w równaniu jako priorytetowe względem dzielenia. Równanie wyglądałoby wtedy:
8÷4(1+1)=? 8÷4(2)=? 8÷8=1
Rozwiązaliście poprawnie to równanie?