Uczeń poprawnie rozwiązał zadania i dostał... 3+. Skorzystał z jednej z żelaznych zasad matematyki
Choć każdy, kto zna tabliczkę mnożenia wie, że mnożenie to działanie, w którym kolejność nie ma znaczenia, za stosowanie się do tej zasady może dostać... obniżoną ocenę. W sieci pojawiło się zdjęcie sprawdzianu z matematyki ocenionego na 3 z plusem, mimo że każde zadanie zostało rozwiązane przez ucznia poprawnie.
Post wywołał wielką dyskusję. Z jednej strony pojawiła się masa komentarzy, że to istna niesprawiedliwość. Że mnożenie jest przemienne, więc to żaden błąd. Że uczeń został zniechęcony do nauki i wmówiono mu, że zrobił coś źle.
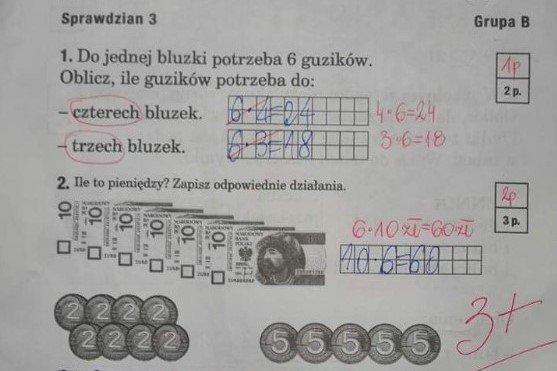
Z drugiej komentujący bronią nauczyciela. "Zapis równania musi zgadzać się z treścią zadania, co w tym dziwnego? Jest sześć banknotów po 10 zł, a nie jak uczeń napisał: 10 banknotów po sześć zł. Tu chodzi o czytanie ze zrozumieniem".
"Ludzie, czy wy naprawdę nie widzicie, że ten sprawdzian dotyczył poprawnego wyniku i poprawnego zapisu mnożenia? Jasne, że 3x4, daje nam tyle samo co 4x3, ale trzy wypłaty po cztery tysiące to nie to samo, co cztery wypłaty po trzy tysiące. Chociaż w jednym i drugim przypadku zarobimy 12 tysięcy, to w trzy miesiące albo w cztery. Jest różnica" - czytamy w komentarzu.
Niby racja, jednak czy intencja sprawdzianu stoi nad żelazną zasadą, która mówi, że mnożenie jest naprzemienne? A co jeśli uczeń z rozmysłem pozamieniał cyfry, bo wiedział, że przecież to bez różnicy czy mnoży 10 zł x 6 sztuk, czy odwrotnie? Teoretycznie w pisemnej odpowiedzi widzimy, że uczeń może mieć problem z rozumieniem treści zadania. Jednak czy to wystarczający powód, by odejmować punkty? Jak sądzicie?
Może cię zainteresować: Uczeń poprawnie rozwiązał zadanie i dostał 0 punktów. Takie rzeczy tylko w polskiej szkole
