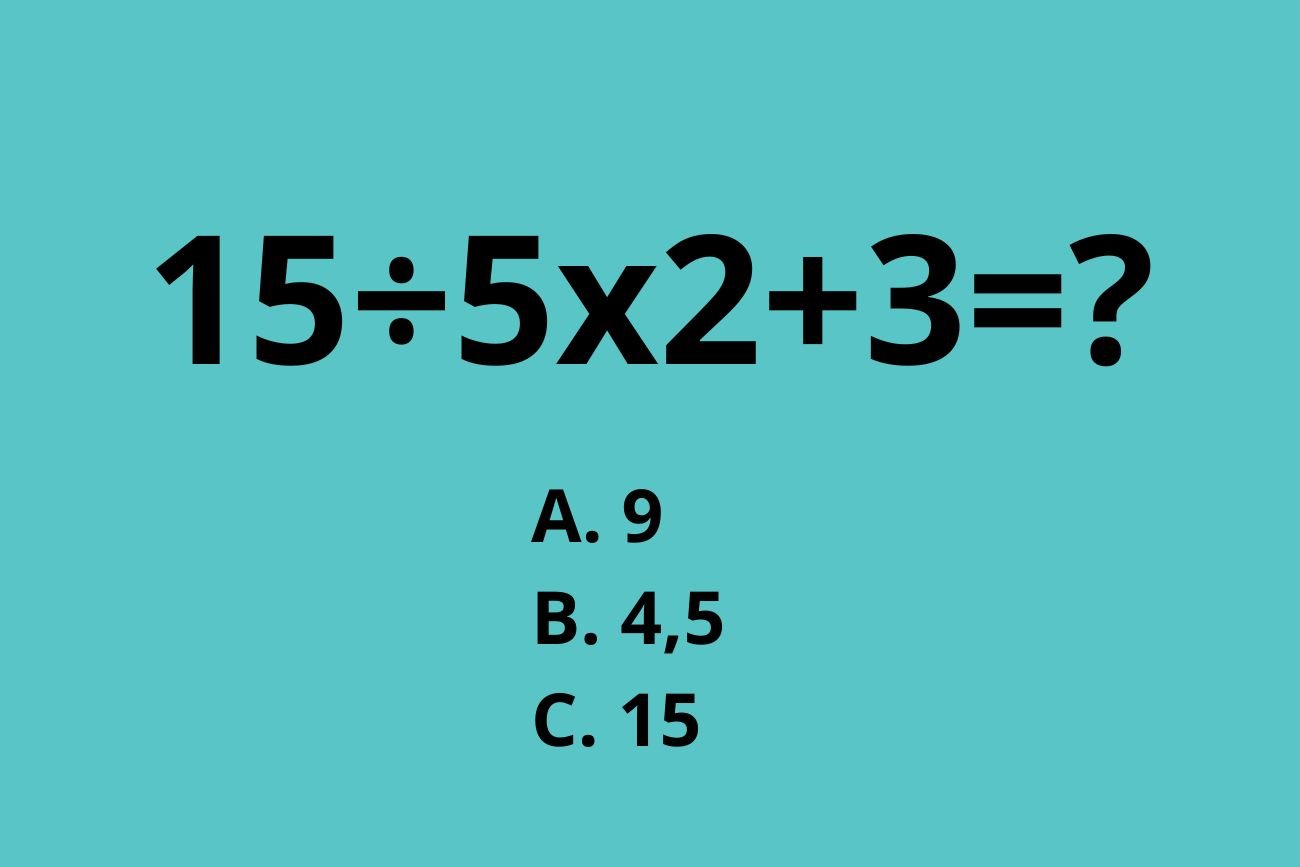
To jedno z tych nieco bardziej podchwytliwych równań matematycznych. Wystarczy jednak przypomnieć sobie ze szkoły kolejność wykonywania działań, by obliczyć je w pamięci w mniej niż 30 sekund. Dlaczego tak wiele osób nie radzi sobie z tą zagadką?
To działanie pojawiło się w teście matematycznym opublikowanym na kanale @puzzlemonster na YouTubie. Test zawiera 15 tego typu równań, jednak właśnie to umieszczono na planszy tytułowej. Obok działania znalazł się napis: "95 proc. nie daje rady tego rozwiązać". To oczywiście bzdura, bo nie wierzę, że aż tyle osób poległoby na tym równaniu, ale rozumiem: takie tytuły się klikają. Hej, sama kliknęłam. I ty chyba też? ;)
Przejdźmy zatem do samego działania. Wiesz, jaka jest prawidłowa odpowiedź? Najczęściej pojawiają się wyniki: 9, 4,5 oraz 15. Prawidłowa jest oczywiście pierwsza odpowiedź, czyli 9. Dlaczego?
Zacznijmy od prawidłowej kolejności wykonywania działań. To równanie jest wyjątkowe, bo jeśli zaczniemy je rozwiązywać od lewej do prawej strony, jakbyśmy czytali książkę, uzyskamy właściwy wynik. To dlatego, że jest zapisane w sposób zgodny z kolejnością działań:
15÷5x2+3=? 3x2+3=? 6+3=9
Prawidłowy wynik to 9. Jeśli nie znamy powyższej zasady i będziemy obliczać to działanie od lewej do prawej strony, również uzyskamy taką odpowiedź. Schody zaczną się w momencie, gdy zaczniemy za bardzo kombinować.
Jeśli z jakiegoś powodu uznamy, że mnożenie jest ważniejsze niż dzielenie i to ono ma pierwszeństwo w obliczeniach, wtedy uzyskamy wynik 4,5. Jeśli najpierw wykonamy dodawanie, a następnie przejdziemy do dzielenia i mnożenia, otrzymamy 15, co również jest błędem. Kombinacji jest wiele, jednak tylko jedna jest właściwa.
A tu możecie zobaczyć film z tym i innymi, podobnymi równaniami:
Dołącz do zamkniętej grupy rodziców na Fb! Tu rozmawiamy i wygrywamy nagrody.